On Soft Clustering for Correlation Estimators

Abstract

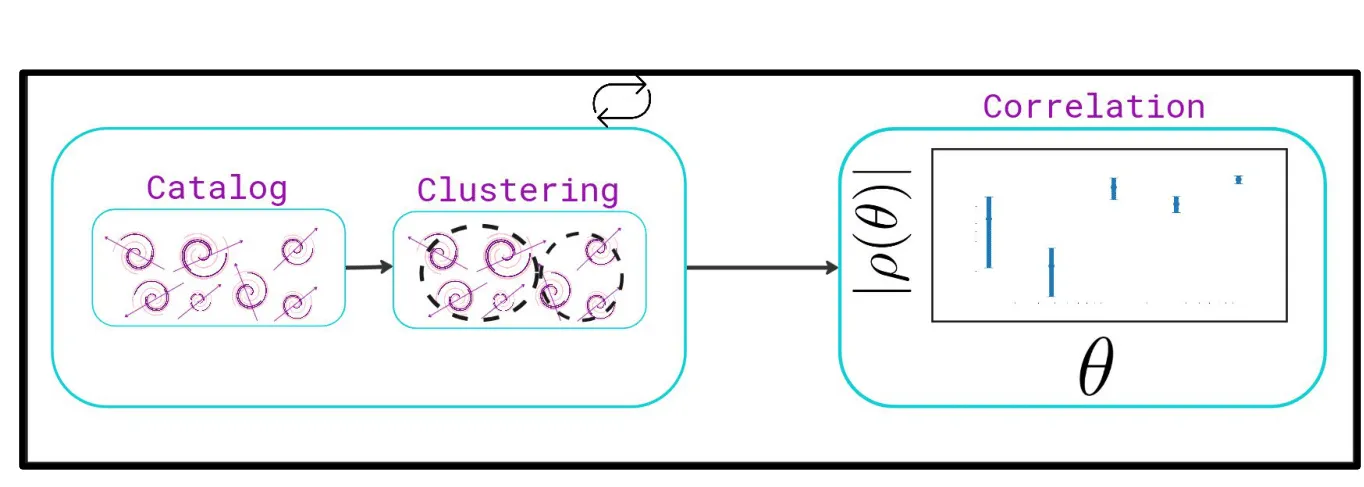
Properly estimating correlations between objects at different spatial scales necessitates $\mathcal{O}(n^2)$ distance calculations. For this reason, most widely adopted packages for estimating correlations use clustering algorithms to approximate local trends. Methods for quantifying the error introduced by clustering have been understudied. In response, we present an algorithm for estimating correlations that is probabilistic in the way that it clusters objects, enabling us to quantify the uncertainty caused by clustering simply through model inference. We also observe that these soft clustering assignments enable correlation estimators that are theoretically differentiable with respect to their input catalogs. Thus, we follow by building up a theoretical framework for differentiable correlation functions and describe their utility in comparison to existing surrogate models. Notably, we find that the repeated use of the normalization and distance function calls makes gradient calculations slow and sparsity patterns in Jacobians that propagate through the chain rule makes the precision unstable, pointing towards either approximate or surrogate methods as a necessary solution to exact gradients from correlation functions. To that end, we close with a discussion of surrogate models as proxies for correlation functions. We provide an example that demonstrates the efficacy of surrogate models to enable gradient based optimization of astrophysical model parameters, successfully minimizing a correlation function output. Our numerical experiments cover science cases across cosmology, from point spread function (PSF) modeling efforts to gravitational simulations to intrinsic alignments (IA). We release the code used in this study at https://github.com/EdwardBerman/cosmo-corr and https://github.com/EdwardBerman/jax-cosmo-corr.

Model Uncertainty

Probabilistic clustering assignments enables us to study epistemic uncertainty in addition to aleatoric uncertainty.

Differentiability

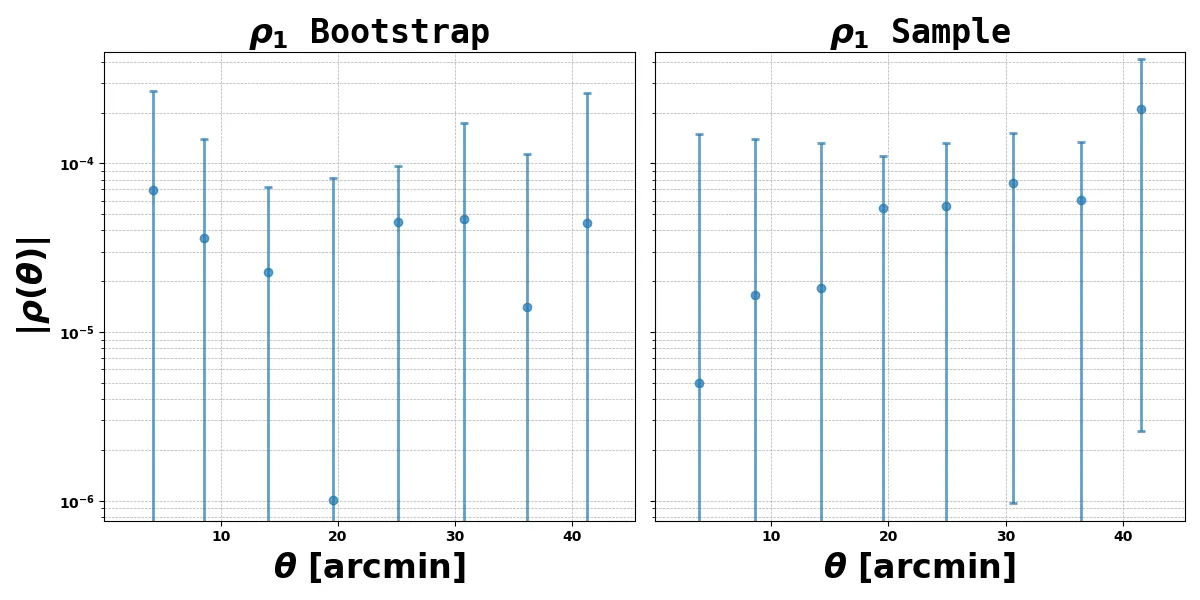
We forward model galaxy evolution with ODEs and show how we can backpropogate a shear-shear correlation all the way through to the underlying physics. The key method is using skip gradients to pass information from objects created from clustering to their constituent galaxies.

Surrogates

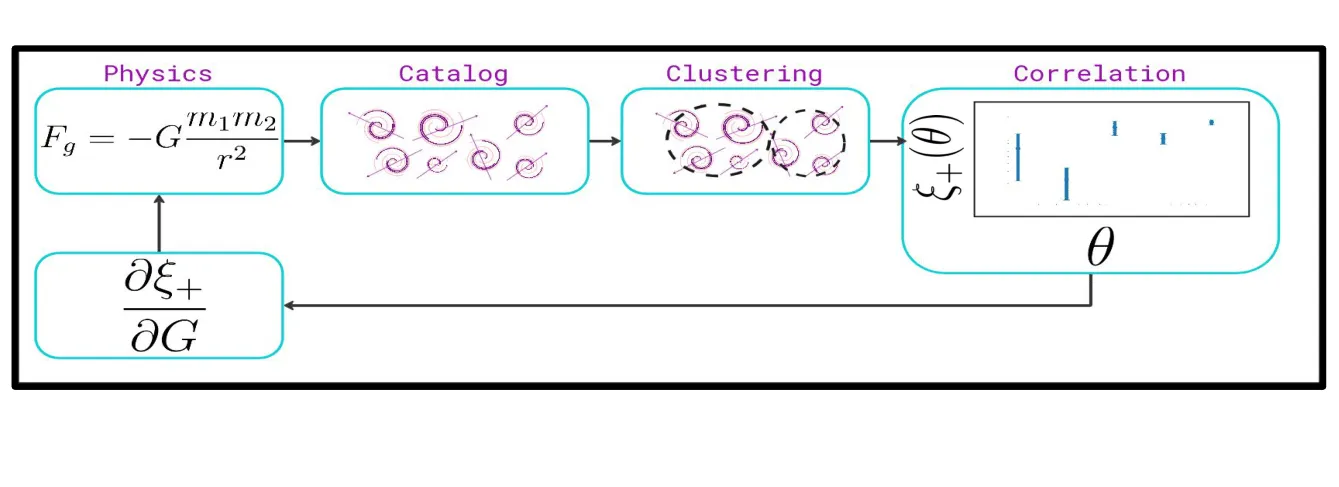
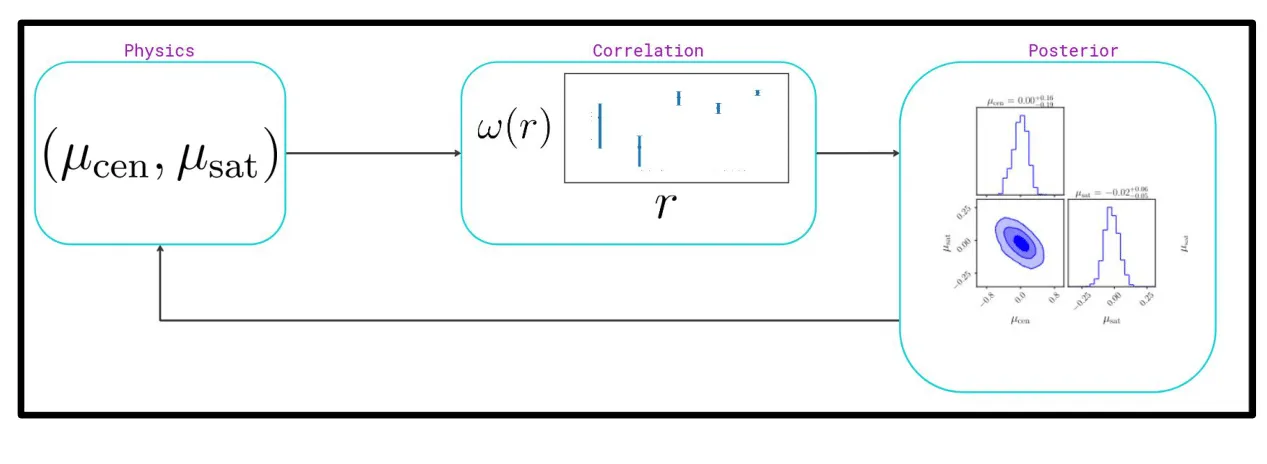
Using surrogates, we have a differential function from the underlying physics straight to the correlation value. We leverage this differentiability to perform Hamiltonian Monte Carlo (HMC) and find posterior distributions over IA parameters most likely to minimize a correlation function.

BibTeX citation

  
  @misc{CosmoCorr,
  author = {Edward Berman},
  title = {CosmoCorr: Cosmological Correlation Function Estimator},
  year = {2024},
  howpublished = {\url{https://github.com/EdwardBerman/CosmoCorr}},
  note = {Accessed: 2024-09-23}
}